Как ни наглядны графики, но по ним не всегда можно находить с достаточной точностью требуемые величины, поэтому при многократном применении графиков может накопиться большая ошибка; в этом отношении, как вы знаете, гораздо удобнее использовать формулы или уравнения. Поэтому Ходжкин и Хаксли постарались описать полученную ими экспериментальную картину математически.
Вы, вероятно, знаете, что кроме методов построения графиков функций по их формулам существуют и методы решения обратной задачи – по графику найти аналитическое выражение для функции, изображаемой этим графиком. Дело облегчается, если известен вид функции; например, известно, что это линейная зависимость. Одни кривые удобно приближать многочленом, другие – тригонометрическими функциями. Удачный подбор приближающих функций иногда помогает выяснить существо изучаемого явления. Например, представив запись вибрации станка в виде суммы синусоидальных кривых, можно выяснить основные причины вибрации.
Ходжкину и Хаксли удалось описать изменение калиевой проницаемости при сдвиге потенциала на мембране с помощью дифференциального уравнения Непрерывные кривые на рис. 20 – решения этого уравнения, а кружочки – результаты экспериментов с фиксацией потенциала, Ясно, что кривая изменения натриевой проницаемости имеет гораздо более сложную форму и должна быть описана иначе. Однако Ходжкин и Хаксли попытались описать и эти графики с помощью уравнений того же вида, который оказался удачным в случае калиевой проницаемости. Для этого они представили изменение натриевой проницаемости как произведение двух функций: одной возрастающей – ее назвали натриевой активацией, другой убывающей – ее назвали натриевой инактивацией. Эти функции удалось описать точно такими же уравнениями, как калиевую проницаемость.
Чтобы понять, как Ходжкин и Хаксли «построили» свою математическую модель процесса возбуждения, разберемся еще чуть подробнее, что же происходит в мембране. Для этого нам придется вернуться к ее электрической схеме, но теперь мы можем внести в нее изменения в соответствии с натриевой теорией возбуждения.
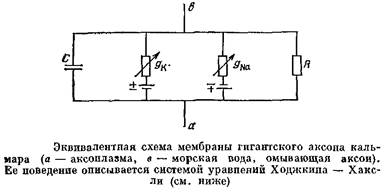
Напомним, что мембрана с электрической точки зрения представляет собой параллельно включенные емкость С и два элемента-источника тока, имеющие противонаправленные э.д.с. и внутренние сопротивления Rk и /? Na – Эти сопротивления являются переменными и определяются калиевой gK и натриевой проводимостями *.)
Рассмотрим вначале калиевый ток. Ионы калия идут через мембрану всегда, причем в обе стороны. Когда потенциал на мембране равен нернстовскому потенциалу, который иначе называют потенциалом равновесия для калия > т0 сохраняется динамическое равновесие, т.е. калиевый ток равен нулю. Если же мембранный потенциал отклоняется от равновесного, то возникает калиевый ток, силу которого можно определить по закону Ома: / = VIR. Заменив HR на калиевую проводимость gK, а. V – на величину отклонения
МП от равновесного, т.е., получаем
Аналогичной формулой определяется и сила натриевого тока:
Здесь Уна – равновесный натриевый потенциал, т.е. неристовский потенциал для натрия, который равен примерно +40 мВ.
Как видно, силы токов зависят от МП довольно сложным образом: V стоит в скобках и, кроме того, входит как аргумент в коэффициенты gк и
Теперь наступает очень важный этап: необходимо замкнуть кольцо обратной связи, учесть, как меняется сам МП в зависимости от изменений проницаемости. И тут выступает на авансцену действующее лицо, пока скромно стоявшее за кулисами, т.е. сбоку нашей схемы, – емкость.
По известной формуле д = УС заряд на конденсаторе равен разности потенциалов на его пластинах, умноженной на его емкость. Продифференцировав это равенство, мы получим
Но это и есть сила тока, поступающего на конденсатор. В нашем случае это сумма натриевого, калиевого токов и тока, подающегося на мембрану извне. Таким образом,
В итоге мы получаем уравнение, определяющее, как меняется мембранный потенциал при изменении проводимостей мембраны и внешнего воздействия:
Полная система уравнений, описывающая все многообразие взаимосвязанных изменений во времени электрических характеристик возбудимой мембраны, такова:
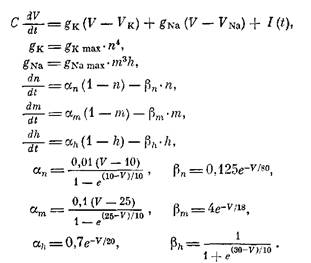
Эта система уравнений и называется моделью Ходжкина – Хаксли, или, сокращенно, моделью X–X.
Вот теперь и стало возможным объяснить возникновение ПД не «на пальцах», как это сделано на с. 88, а строго математически. И хотя эту систему оказалось невозможным решить в явном виде, т.е., например, найти зависимость потенциала от времени в виде V = = V, в математике существовали методы, которые позволяли вычислять значения этих функций для любых конкретных условий *), находя последовательно значения, которые принимает V с течением времени.
Прочие статьи:
Связь поверхностного натяжения с адсорбцией
Рассмотрим соотношение между адсорбцией и поверхностным натяжением в рамках теории регулярных растворов. Для обсуждения адсорбции растворенного вещества на поверхности жидкость-воздух необходимо определить, что такое поверхность. Первое о ...
Раса как морфофизиологическое понятие
Основными критериями подразделения человечества на расы всегда были внешние особенности строения тела, Иными словами, с самого начала истории антропологии для выделения рас использовали морфологические признаки. Сами расы рассматривали ка ...
Естественный отбор
Однако о правильности постулатов генетики должно быть сказано гораздо больше. Далекие от того, чтобы поддержать эволюционную теорию, исследования последних семидесяти лет приводят к единственному выводу: эволюция происходить не могла, ...